首页 / 教程
wps做灰色关联分析 | 灰色关联分析法的具体计算步骤
2022-12-13 03:05:00
1.灰色关联分析法的具体计算步骤
(1)确定反映系统行为特征的参考数列和影响系统行为的比较数列
反映系统行为特征的数据序列,称为参考数列。影响系统行为的因素组成的数据序列,称比较数列。
(2)对参考数列和比较数列进行无量纲化处理
由于系统中各因素的物理意义不同,导致数据的量纲也不一定相同,不便于比较,或在比较时难以得到正确的结论。因此在进行灰色关联度分析时,一般都要进行无量纲化的数据处理。
(3)求参考数列与比较数列的灰色关联系数ξ(Xi)
所谓关联程度,实质上是曲线间几何形状的差别程度。因此曲线间差值大小,可作为关联程度的衡量尺度。对于一个参考数列X0有若干个比较数列X1, X2,…, Xn,各比较数列与参考数列在各个时刻(即曲线中的各点)的关联系数ξ(Xi)可由下列公式算出:其中 ρ为分辨系数,一般在0~1之间,通常取0.5。
是第二级最小差,记为Δmin。 是两级最大差,记为Δmax。
为各比较数列Xi曲线上的每一个点与参考数列X0曲线上的每一个点的绝对差值,记为Δoi(k)。
所以关联系数ξ(Xi)也可简化如下列公式:
(4)求关联度
因为关联系数是比较数列与参考数列在各个时刻(即曲线中的各点)的关联程度值,所以它的数不止一个,而信息过于分散不便于进行整体性比较。因此有必要将各个时刻(即曲线中的各点)的关联系数集中为一个值,即求其平均值,作为比较数列与参考数列间关联程度的数量表示,关联度 公式如下:
ri--比较数列xi对参考数列x0的灰关联度,或称为序列关联度、平均关联度、线关联度。
ri值越接近1,说明相关性越好。
(5)关联度排序
因素间的关联程度,主要是用关联度的大小次序描述,而不仅是关联度的大小。将m个子序列对同一母序列的关联度按大小顺序排列起来,便组成了关联序,记为{x},它反映了对于母序列来说各子序列的“优劣”关系。若r0i>r0j,则称{xi}对于同一母序列{x0}优于{xj},记为{xi}>{xj} ;r0i表示第i个子序列对母数列特征值。
灰色关联度分析法是将研究对象及影响因素的因子值视为一条线上的点,与待识别对象及影响因素的因子值所绘制的曲线进行比较,比较它们之间的贴近度,并分别量化,计算出研究对象与待识别对象各影响因素之间的贴近程度的关联度,通过比较各关联度的大小来判断待识别对象对研究对象的影响程度。
2.灰色关联分析方法如何计算
灰关联分析的具体计算步骤如下:
(1)确定反映系统行为特征的参考数列和影响系统行为的比较数列
反映系统行为特征的数据序列,称为参考数列。影响系统行为的因素组成的数据序列,称比较数列。
(2)对参考数列和比较数列进行无量纲化处理
由于系统中各因素的物理意义不同,导致数据的量纲也不一定相同不便于比较,或在比较时难以得到正确的结论。因此在进行灰色关联度分析时,一般都要进行无量纲化的数据处理。
(3)、求差序列(4)、求两级最大差与最小差(5)、求关联系数(6)、计算关联度
我自己在word中编辑的公式粘贴不过来
3.灰色关联分析法,具体的例子说明如何运用灰色关联分析法
灰色关联分析是根据因素之间发展趋势的相似或相异程度,即“灰色关联度”作为衡量因素间关联程度的一种方法。计算步骤:
(1)确定反映系统行为特征的参考数列和影响系统行为的比较数列。
(2)对参考数列和比较数列进行无量纲化处理
(3)求参考数列与比较数列的灰色关联系数ξ(Xi)
(4)求关联度ri
(5)排关联序
你是想对制造业信息化进行投入产出分析是非常有意义的,也具有一定难度。并想利用灰色关联法对制造业信息化进行投入产出分析,关键是能否应用?有无结合的必要。从你设置的20个因素主要体现企业信息化在软硬件设施投入、信息化资金投入、信息化人力资源投入、网络建设投入、信息安全投入、企业电子商务投入等信息来看,考虑的比较全面,那么制造业信息化的产出是什么也要很好的考虑,然后再对制造业信息化进行比较全面的投入产出分析。
信息化的投入到底能够给企业带来什么回报,是所有的企业决策者在做出信息化投入决策之前最关心的事情。你需要考虑信息化所带来的有形和无形的收益。一般讲,信息化投资带来的回报主要体现在两个方面:为企业带来收入的增加和成本的降低,因此可以简单地描述ROI的计算,公式为:ROI=(节省的成本+增加的收益)/方案投资,或者ROI=回报/在规定的时间内如1、3、5年内的投资总额, 但是在今天愈加复杂的企业环境下,实际的ROI计算要比上述公式复杂得多。在计算ROI的时候,投入的成本容易计算,但是带来的收益较难预测,但可以分析。产出的多少不仅依赖于投入的多少,还依赖于投入产出的效率。提高投入产出效率,可以在信息化投入相对有限的情况下提高信息化水平。可以考虑制造业信息化的投入对企业产出及效益的投入产出效率、综合有效性、纯技术有效性、规模有效性和规模效益都可进行分析。制造业信息化是以信息化带动工业化的突破口,是提高我国制造业国际竞争能力的客观需要,故你要抓住对制造业信息化进行投入产出分析这个主题下功夫。
至于灰色关联法主要是利用“灰色关联度”来衡量因素间关联程度的一种方法,对你分析的主题似乎作用不是很大。如你要考虑制造业信息化对国民经济发展的关联问题,最好运用投入产出理论,利用编制的投入产出表计算,可揭示深层次的制造业信息化投入产出技术经济联系。见解不一定对,请你考虑。祝你成功!
4.灰色关联分析法的介绍
对于两个系统之间的因素,其随时间或不同对象而变化的关联性大小的量度,称为关联度。在系统发展过程中,若两个因素变化的趋势具有一致性,即同步变化程度较高,即可谓二者关联程度较高;反之,则较低。因此,灰色关联分析方法,是根据因素之间发展趋势的相似或相异程度,亦即“灰色关联度”,作为衡量因素间关联程度的一种方法。
5.灰色关联度的程序如何求
根据科学出版社2004年11月出版,由刘思峰、党耀国、方国耕三人编写的《灰色系统理论及其应用(第三版)》中所述,灰色关联度分析是从属于灰色系统理论这一新学科。
此书全面、系统地论述了灰色系统的基本理论、基本方法和应用技术,是作者长期从事灰色系统理论探索、实际应用和教学工作的结晶,同时还吸收了国内外同行近年来取得的理论和应用研究新成果,向读者展示出灰色系统理论这一新学科的概貌以及发展动态。 全书共14章,包括灰色系统的基本概念与基本原理、灰色方程与灰色矩阵、序列算子与灰色序列生成、灰色关联分析、灰色聚类评估、灰色系统建模、灰色系统预测、灰色组合模型、灰色决策、灰色规划、灰色投人产出、灰矩阵博奕模型和灰色控制等内容,并附有灰色建模系统软件包。
其中序列算子、缓冲算子公理系统及系列化弱化和强化算子、灰数灰度测度公理、广义灰色关联度(灰色绝对关联度、灰色相对关联度、灰色综合关联度)、定权灰色聚类评估和基于三角白化权函数的灰评估新方法、LPGP漂移与定位求解、GM(1,1)模型的适用范围以及灰色经济计量银型(G-E)、灰色生产函数模型(G-C-D)、灰色投人产出模型(G-I-O)、灰色马尔可夫模型(G-M)和灰色解模型(G-G)等系作者首次提出。 希望我的回答对你有用。
6.基于灰色关联分析的几种决策方法及其应用
多属性决策方法己经成功地应用于工程、经济、市场分析、管理等实际问题中。人们时常要面对众多指标,从许多可供选择的方案中做出决策,也就是要对所有的方案进行比较、排序或择优。对多属性决策方法进行系统深入的研究对于解决实际问题具有重要的意义。本文在深入分析主成分分析、理想解法等经典决策方法的基础上,引入灰色系统理论,基于灰色关联分析提出了几种决策模型,为贫信息环境下的决策问题提供了几点新思路。
基于灰色关联分析系数矩阵和理想解法,提出了一种新的理想解法。该方法以原始数据样本与理想方案之间的灰色关联系数矩阵为新的决策矩阵,利用理想解法对方案进行排序。克服了传统理想解法仅仅基于原始数据,难以挖掘数据内在规律的缺点,为有限样本条件下的决策问题提供了一种新思路。
将主成分分析和灰色关联聚类分析相结合提出了基于灰色关联聚类分析和主成分分析的决策方法,在进行多指标分析和评价的过程中,首先对指标进行灰色关联聚类分析,将指标分成若干可以定义的类,每个聚类代表同一类指标;其次对每个聚类进行主成分分析,提取主成分,获得该类指标的主成分集合;最后基于权重思想综合所有聚类的主成分集合,形成既反映全体指标信息又体现指标聚类差异性的综合指标。通过一个算例说明该方法计算方便,客观合理。
引入灰色系统理论对传统理想解法(TOPSIS)进行了拓展,提出了一种基于组合权重的灰色关联理想解法(GC-TOPSIS)。首先利用AHP和熵值法对决策指标进行组合赋权,其次依据灰色关联分析理论,以灰色关联度为决策单元构造GC-TOPSIS模型,最后通过一个供应商选择的实例验证了方法的有效性和可行性。
建立了基于灰色关联度和理想解法的决策方法。该方法将欧氏距离和灰色关联度有机结合,构造了一种新的相对贴近度以实现对方案的评价。新贴近度同时反映了方案与理想方案和负理想方案之间的位置关系和数据曲线的相似性差异,物理含义更加明确。最后仍然通过供应商选择的示例进一步说明了方法的应用步骤。
硕士研究生:孙晓东(管理科学与工程)指导教师:胡劲松教授
7.WPS里如何改变灰色背景颜色
初始表格
选中表格
点击背景填充选项,选择无填充颜色
无填充色表格
最新内容
| 手机 |
相关内容
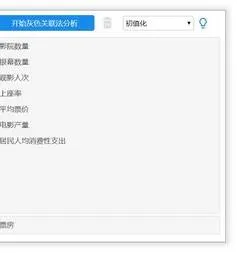
windows10中设置 【Windows10中设
windows10中设置 【Windows10中设置用户账户的方法】,设置,方法,用户账户,点击,控制面板,界面,Win10下设置切换输入法需要打开电脑
windows10合盘步骤 【window10系统
windows10合盘步骤 【window10系统怎么合盘】,合盘,系统,步骤,镜像,磁盘,删除,1、右键点一下“此电脑”,在弹出的右键菜单中选择“管
wps文档设置下页标题栏 | wps凡是
wps文档设置下页标题栏 【wps凡是有标题一的都另起一页,设置方法求高手】,设置,标题栏,表格,文档,方法,高手,1.wps凡是有标题一的都
wps表格计算时间差 | WPSoffice201
wps表格计算时间差 【WPSoffice2012个人版WPS表格计算时间差啊】,计算,表格,日期,个人版,单元,表格中,1.WPS office 2012个人版 WPS
wps复制带公式的数据库 | wps只复
wps复制带公式的数据库 【wps只复制公示计算出来的数据】,计算,复制,数据,公式,教程,数据库,1.wps怎样只复制公示计算出来的数据1.
在wps中四舍五入 | wps或excel中将
在wps中四舍五入 【wps或excel中将计算式四舍五入取整】,四舍五入,取整,表格,示例,教程,函数,1.wps或excel中如何将计算式四舍五入
wps表格中计算自然对数 | 用WPS表
wps表格中计算自然对数 【用WPS表格将数据换算成对数】,计算,表格,函数,数据,用于,函数公式,1.如何用WPS表格将数据换算成对数打开E
wps固定函数计算 | WPS在文字的表
wps固定函数计算 【WPS在文字的表格中进行函数公式计算】,计算,函数,公式计算,表格中,公式,锁定,1.WPS如何在文字的表格中进行函数